Zeitpläne
Curo Rechner bietet zwei unterschiedliche Arten von Zeitplänen: den Amortisationsplan und den EAR/APR-Nachweis. Die Wahl der Tagszählkonvention auf der Eingabeseite bestimmt, welcher Zeitplan Ihre Berechnungsergebnisse begleitet – zugänglich auf dem zweiten Tab des Ergebnisbildschirms. Hier die Aufschlüsselung:
Amortisationsplan: Wird für alle standardmäßigen Tagszählkonventionen generiert (z. B. 30/360, Actual/Actual). Dieser Plan detailliert jede Zahlung eines Kredits und zeigt, wie sich jede Rate auf Zinsen und Tilgung aufteilt. Besonders nützlich für Geschäftskunden, die ihre Buchhaltung mit genauen Zahlungsaufteilungen aktualisieren müssen.
EAR/APR-Nachweis: Wird bei Konventionen mit EAR- oder APR-Suffix erzeugt (z. B. US Appendix J APR, EU 2023/2225 APR). Dieser Plan demonstriert die Berechnungsmethode hinter dem Zinssatz und verifiziert dessen Genauigkeit, indem alle diskontierten Vorschüsse, Zahlungen und Gebühren sich auf null summieren. Unverzichtbar für Kreditgeber und -nehmer, die den angegebenen Zinssatz validieren oder anfechten müssen.
Aus Sicht von Curo Rechner dienen diese Pläne dazu:
- Ergebnisse in leicht verständlicher Form darzustellen.
- Schnell zu prüfen, ob Ihre Eingaben das erwartete Tilgungsprofil ergeben, besonders bei komplexen Szenarien mit mehreren Variablen.
- Die Validierung eines Zinssatzergebnisses, falls erforderlich.
Alle Plan-Daten können im XLSX (Tabellenkalkulationsformat) heruntergeladen werden. Klicken Sie einfach auf die Download-Schaltfläche oben auf jedem Plan.
Wenn ein Plan Zahlungen am selben Datum enthält, erscheint oben eine Zahlungen bündeln-Schaltfläche. Schalten Sie diese um, um Zahlungen am selben Datum zu bündeln oder aufzutrennen – für eine übersichtlichere Darstellung. Probieren Sie dies in den Beispielen 07 und 09 aus.
Der folgende Abschnitt erklärt detailliert, wie Sie jedes von Curo Rechner erzeugte Zinssatzergebnis mit den Daten aus diesen Plänen validieren können. Dieser Teil ist recht technisch und richtet sich vor allem an Nutzer, die tiefer einsteigen möchten.
Validierung des Zinssatzes
EAR/APR-Nachweis
Der EAR/APR-Nachweis verwendet je nach gewählter APR-Konvention eine von zwei Diskontierungsmethoden zur Validierung des Zinssatzes:
- Standard-APR-Konventionen (z. B. EU 2023/2225 APR): Verwenden eine Standard-Diskontierungsformel und zeigen in der Spalte Diskontierungseingaben den Faktor ( $t$ ) für jede Zeile.
- US Appendix J APR: Verwendet eine US-spezifische Diskontierungsformel (aktuarische Methode) und zeigt in der Spalte Diskontierungseingaben die Parameter ( $f$ ), ( $t$ ) und ( $p$ ) für jede Zeile.
Nachfolgend ein vereinfachtes Beispiel für jede Methode zur Veranschaulichung.
Standard-APR-Konventionen
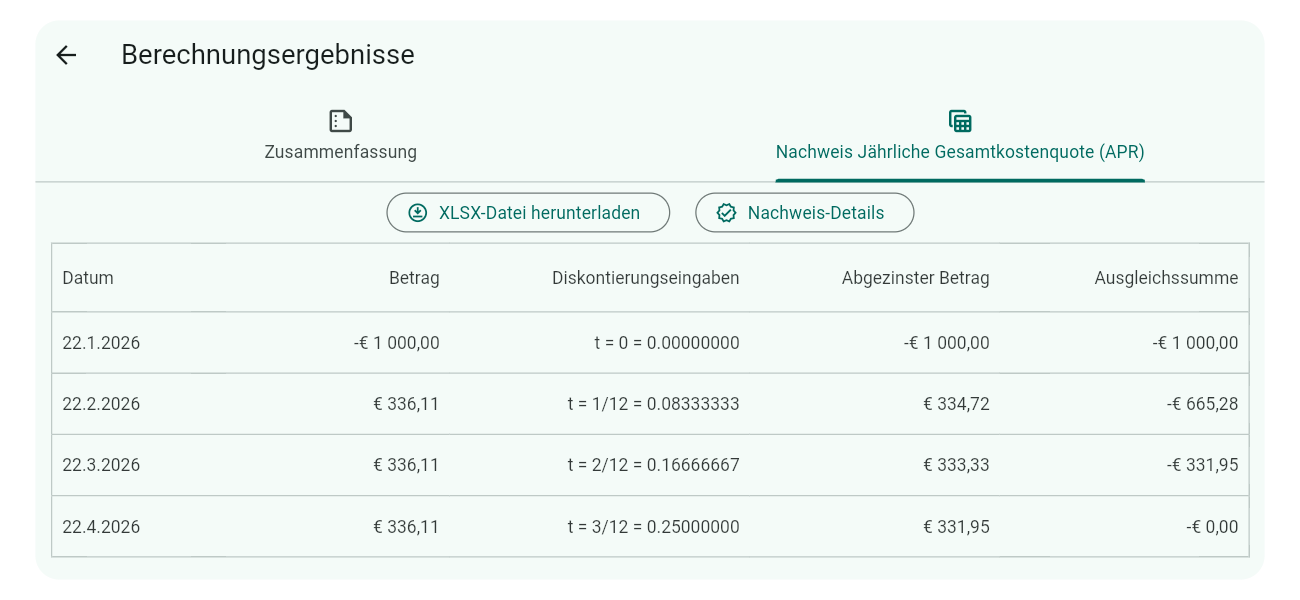
Bei Standard-APR-Konventionen zeigt die Spalte Diskontierungseingaben ( $t$ ), den Zeitfaktor für die Diskontierung. Hier ein Beispielplan:
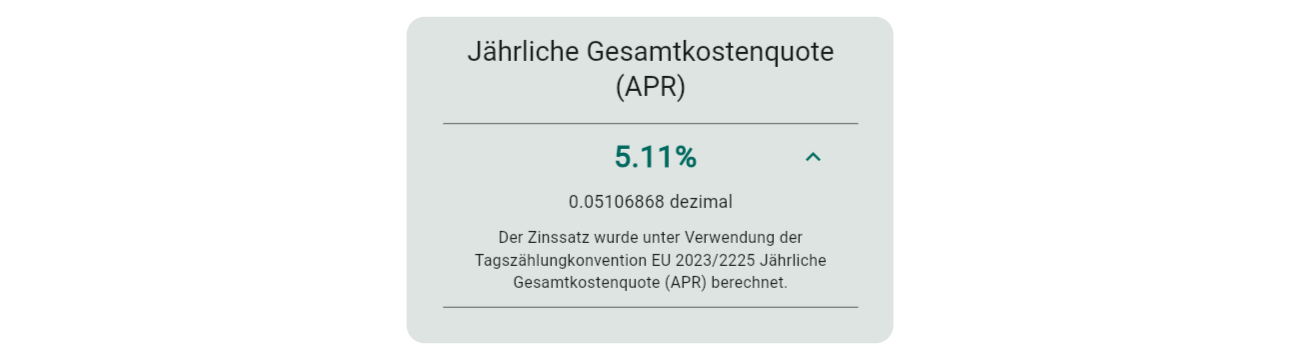
Der zu validierende Zinssatz befindet sich im Ergebnis-Zusammenfassungstab:
Um zu beweisen, dass der Zinssatz (5,11 %) korrekt ist, diskontieren Sie jeden Betrag in der Spalte Amount mit den Diskontierungseingaben ( $t$ ) und dem jährlichen Zinssatz (als Dezimal), und summieren Sie die Ergebnisse. Die Diskontierungsformel und Beispielberechnungen:
Standard-APR-Diskontierungsformel
$$ d = a \times (1 + i)^{-t} $$ wobei:
- ( $d$ ) = Diskontierter Betrag
- ( $a$ ) = Betrag aus dem Plan
- ( $i$ ) = Jährlicher Zinssatz (Dezimal) aus den Ergebnissen
- ( $t$ ) = Periodenfaktor aus dem Plan
| Zeile | Formelberechnung | Diskontierter Betrag ( $d$ ) | Ausgleichssumme |
|---|---|---|---|
| 1 | $$-1000.00 \times (1 + 0.05106868)^{-0.00000000}$$ | -1000.00 | -1000.00 |
| 2 | $$336.11 \times (1 + 0.05106868)^{-0.08333333}$$ | 334.72 | -665.28 |
| 3 | $$336.11 \times (1 + 0.05106868)^{-0.16666667}$$ | 333.33 | -331.95 |
| 4 | $$336.11 \times (1 + 0.05106868)^{-0.25000000}$$ | 331.95 | -0.00 |
Die Spalte Ausgleichssumme führt eine laufende Summe, die auf null reduzieren sollte (kleine Abweichungen ±0,01 durch Rundung möglich). Hier -0,00 – bestätigt den Zinssatz 0.05106868 (5,11 %) für die EU 2023/2225 APR-Konvention.
US Appendix J APR
Bei der US Appendix J APR-Konvention zeigt die Spalte Diskontierungseingaben ( $f$ ) (Odd-Days-Faktor), ( $t$ ) (Einheitenzeitfaktor) und ( $p$ ) (Einheitenperioden pro Jahr). Beispiel für einen Kredit mit drei monatlichen Raten:
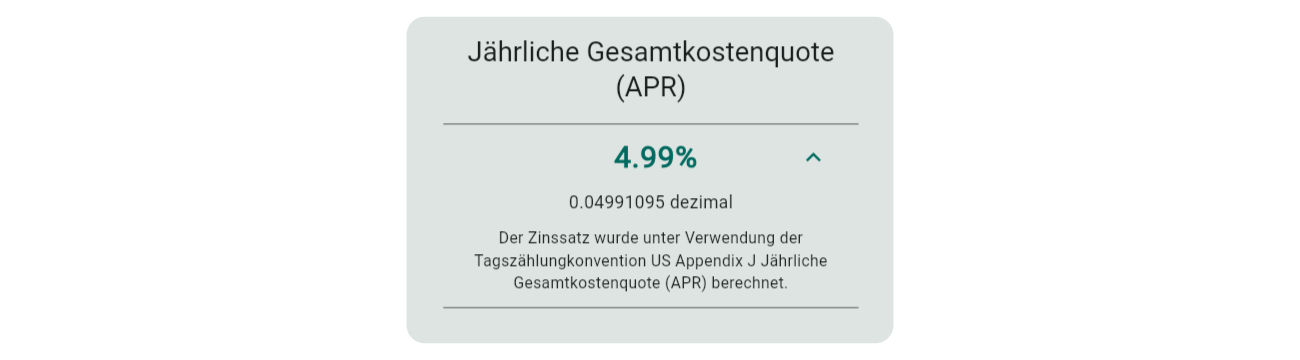
Der zu validierende Zinssatz:
Zur Validierung des jährlichen Zinssatzes (4,99 %) diskontieren Sie jeden Betrag mit ( $f$ ), ( $t$ ), ( $p$ ) und ( $i$ ) (Dezimal).
Diskontierungsformel und Berechnungen:
US Appendix J APR-Diskontierungsformel
$$ d = \frac{a}{(1 + f\frac{i}{p})(1 + \frac{i}{p})^t} $$ wobei:
- ( $d$ ) = Diskontierter Betrag
- ( $a$ ) = Betrag aus dem Plan
- ( $i$ ) = Jährlicher Zinssatz (Dezimal)
- ( $p$ ) = Anzahl Einheitenperioden pro Jahr aus dem Plan
- ( $f$ ) = Zusätzliche Tage innerhalb einer Einheitenperiode aus dem Plan
- ( $t$ ) = Anzahl vollständiger Einheitenperioden aus dem Plan
| Zeile | Formelberechnung | Diskontierter Betrag ( $d$ ) | Ausgleichssumme |
|---|---|---|---|
| 1 | $$\frac{-1000.00}{(1 + 0 \times \frac{0.04991094}{12})(1 + \frac{0.04991094}{12})^0}$$ | -1000.00 | -1000.00 |
| 2 | $$\frac{336.11}{(1 + 0 \times \frac{0.04991094}{12})(1 + \frac{0.04991094}{12})^1}$$ | 334.72 | -665.28 |
| 3 | $$\frac{336.11}{(1 + 0 \times \frac{0.04991094}{12})(1 + \frac{0.04991094}{12})^2}$$ | 333.33 | -331.95 |
| 4 | $$\frac{336.11}{(1 + 0 \times \frac{0.04991094}{12})(1 + \frac{0.04991094}{12})^3}$$ | 331.95 | -0.00 |
Die Spalte Ausgleichssumme führt eine laufende Summe, die auf null reduzieren sollte (kleine Abweichungen ±0,01 durch Rundung möglich). Hier -0,00 – bestätigt den Zinssatz 0.04991094 (4,99 %) für die US Appendix J APR-Konvention.
Amortisationsplan
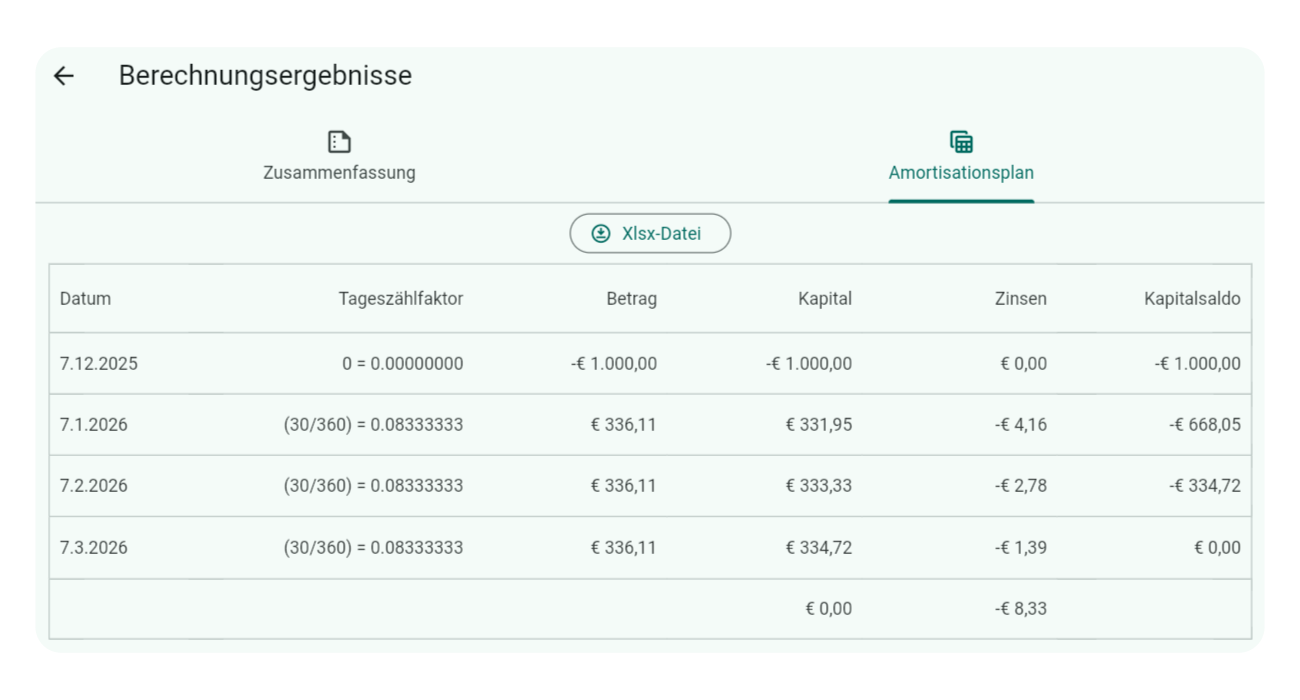
Zur Validierung ein vereinfachtes Beispiel:
Beachten Sie die zusätzliche Spalte nach Datum, die Diskontierungseingaben zeigt. Standardmäßig versteckt (kann verwirrend sein). Zum Anzeigen 3-mal auf den Spaltentitel Datum tippen/klicken. Wiederholen zum Verstecken.
Der zu validierende Zinssatz:
Zur Bestätigung von 4,99 % berechnen Sie periodische Zinsen, addieren zu Kapitalvortrag und Betrag für Kapitalfortrag. Wiederholen bis Ende.
Periodische Zinsformel und Berechnungen:
Periodische Zinsformel
$$ a = c \times i \times f $$ wobei:
- ( $a$ ) = Zinsen (periodisch)
- ( $c$ ) = Kapitalsaldo (Vortrag)
- ( $i$ ) = Jährlicher Zinssatz (Dezimal)
- ( $f$ ) = Tagszählfaktor aus dem Plan
| Zeile | Vortrag ( $c$ ) | Zinsberechnung $$( c \times i \times f )$$ | Betrag | Kapitalsaldo |
|---|---|---|---|---|
| 1 | 0.00 | $$0.00 \times 0.04991095 \times 0.00000000 = 0.00$$ | -1000.00 | -1000.00 |
| 2 | -1000.00 | $$-1000.00 \times 0.04991095 \times 0.08333333 = -4.16$$ | 336.11 | -668.05 |
| 3 | -668.05 | $$-668.05 \times 0.04991095 \times 0.08333333 = -2.78$$ | 336.11 | -334.72 |
| 4 | -334.72 | $$-334.72 \times 0.04991095 \times 0.08333333 = -1.39$$ | 336.11 | 0.00 |
Endgültiger Kapitalsaldo idealerweise null (kleine Rundungsabweichungen erlaubt) – bestätigt 0.04991095 (4,99 %) für 30/360.
Tipp
Auch ohne Validierungsinteresse kann die Diskontierungseingaben-Spalte hilfreich sein, um zu sehen, wie Tagszählungen in Ihrer Konvention verwendet werden. Der Faktor basiert auf der Dauer zwischen aktueller und vorheriger Zahlung.