Schedules
Curo Calculator offers two distinct types of schedules: the Amortisation Schedule and the EAR/APR Proof. The choice of day count convention you make on the input dictates which schedule will accompany your calculation results, accessible on the second tab of the results screen. Here’s the breakdown:
Amortisation Schedule: Generated for all standard day count conventions (e.g., 30/360, Actual/Actual), this schedule details each payment on a loan, showing how each instalment is split between interest and principal reduction. This is particularly beneficial for business borrowers who need to update their financial accounts with precise payment allocations.
EAR/APR Proof: Produced when using conventions with an EAR or APR suffix (e.g., US Appendix J APR, EU 2023/2225 APR), this schedule demonstrates the calculation methodology behind the rate and verifies its accuracy by ensuring that all discounted advances, payments, and charges net out to zero. It’s invaluable for both lenders and borrowers who need to validate or dispute the interest rate applied to a loan.
From a Curo Calculator perspective, these schedules serve to:
- Present results in an easily digestible format.
- Allow you to quickly sense-check if your calculation inputs yield the expected repayment profile, particularly in complex scenarios with multiple variables.
- Enable validation of an interest rate result when necessary.
All schedule data can be downloaded in XLSX (spreadsheet) format for your records or further analysis. Simply click the download button at the top of each schedule.
When a schedule contains same-dated payments, a Bundle Payments button appears at the top. Toggle this button to bundle or unbundle same-dated payments for a cleaner, more organized display. Explore this feature in examples 07 and 09.
The following section delves into how to validate any interest rate result produced by Curo Calculator using the data provided in these schedules. This part gets quite technical and might primarily interest those seeking a deep dive.
Interest Rate Validation
EAR/APR Proof
The EAR/APR Proof schedule uses one of two discount approaches to validate the interest rate, depending on the selected APR convention:
- Standard APR Conventions (e.g., EU 2023/2225 APR): These use a standard discount formula and display a Discount Inputs column with the factor ( $t$ ) for each row.
- US Appendix J APR: This uses a U.S.-specific discount formula, reflecting the actuarial method, and displays a Discount Inputs column with parameters ( $f$ ), ( $t$ ) and ( $p$ ) for each row.
Below, we provide a simplified example for each approach to illustrate the validation process.
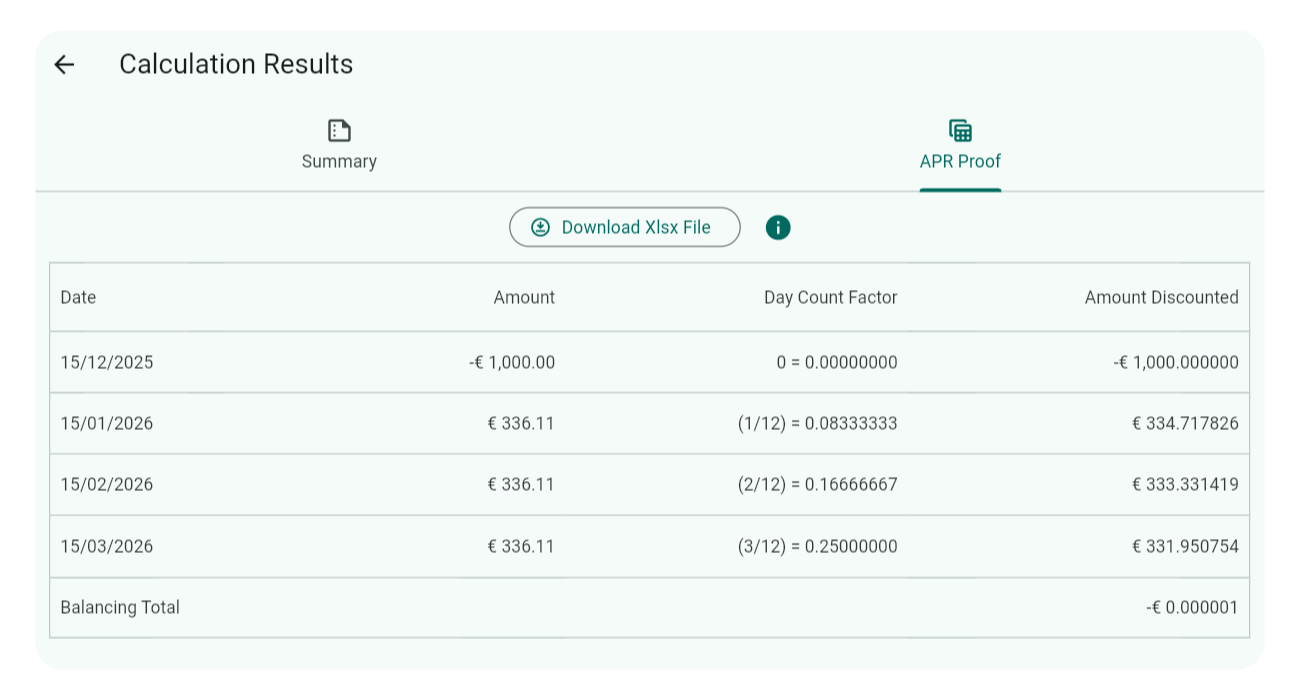
Standard APR Conventions
For standard APR conventions, the proof schedule includes a Discount Inputs column showing ( $t$ ), the time factor for discounting. Below is an example schedule:
The interest rate to validate is found under the result summary tab:
To prove the interest rate (5.11%) is accurate, discount each value in the Amount column using the Discount Inputs ( $t$ ) and the annual interest rate (as a decimal), then sum the results. The discount formula and example calculations are provided below:
Standard APR discount formula
$$ d = a \times (1 + i)^{-t} $$ where:
- ( $d$ ) = Amount Discounted
- ( $a$ ) = Amount (to be discounted) from the schedule
- ( $i$ ) = Annual interest rate (decimal) from summary results
- ( $t$ ) = Periodic factor from the schedule
| Row | Formula Calculation | Amount Discounted ( $d$ ) | Balancing Total |
|---|---|---|---|
| 1 | $$-1000.00 \times (1 + 0.05106868)^{-0.00000000}$$ | -1000.00 | -1000.00 |
| 2 | $$336.11 \times (1 + 0.05106868)^{-0.08333333}$$ | 334.72 | -665.28 |
| 3 | $$336.11 \times (1 + 0.05106868)^{-0.16666667}$$ | 333.33 | -331.95 |
| 4 | $$336.11 \times (1 + 0.05106868)^{-0.25000000}$$ | 331.95 | -0.00 |
The Balancing Total column maintains a running total that should reduce to zero, though minor variations (±0.01) may occur due to rounding. Here, the total is -0.00, confirming the interest rate of 0.05106868 (5.11%) is correct for the EU 2023/2225 APR convention.
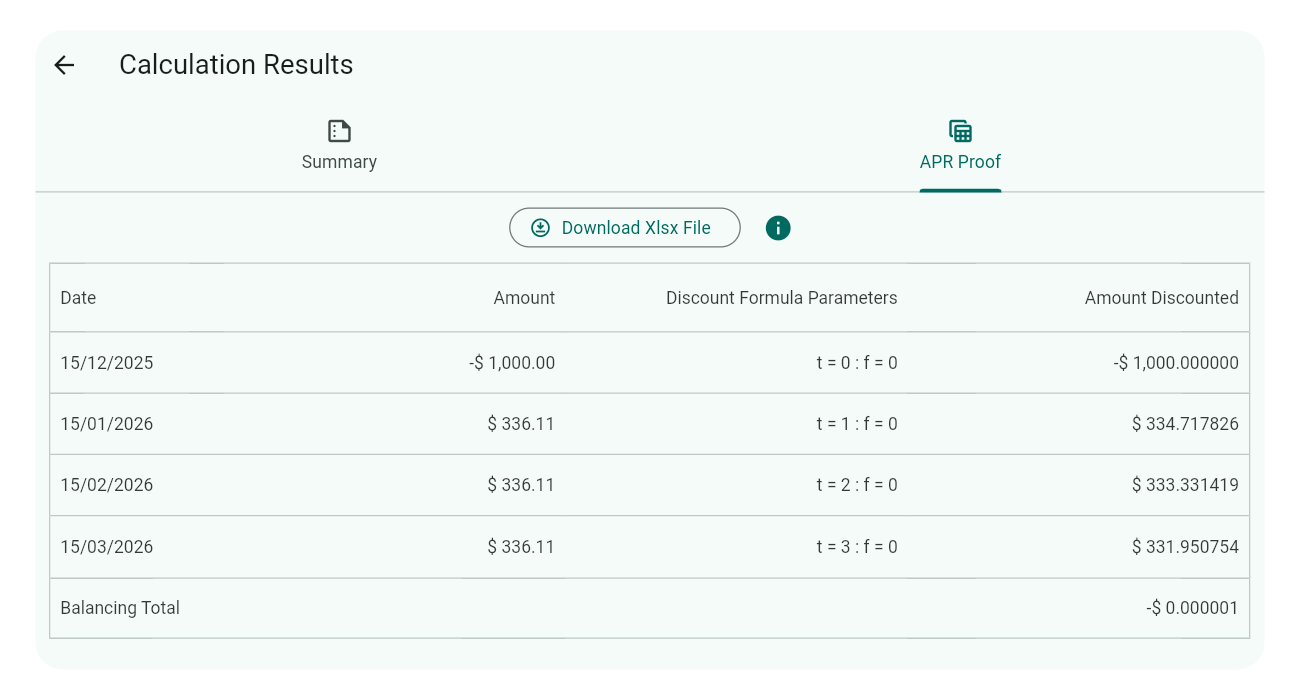
US Appendix J APR
For the US Appendix J APR convention, the proof schedule includes a Discount Inputs column showing ( $f$ ) (odd-days factor), ( $t$ ) (unit-period time factor) and ( $p$ ) (unit-periods in a year). Below is an example schedule for a loan with three monthly repayments:
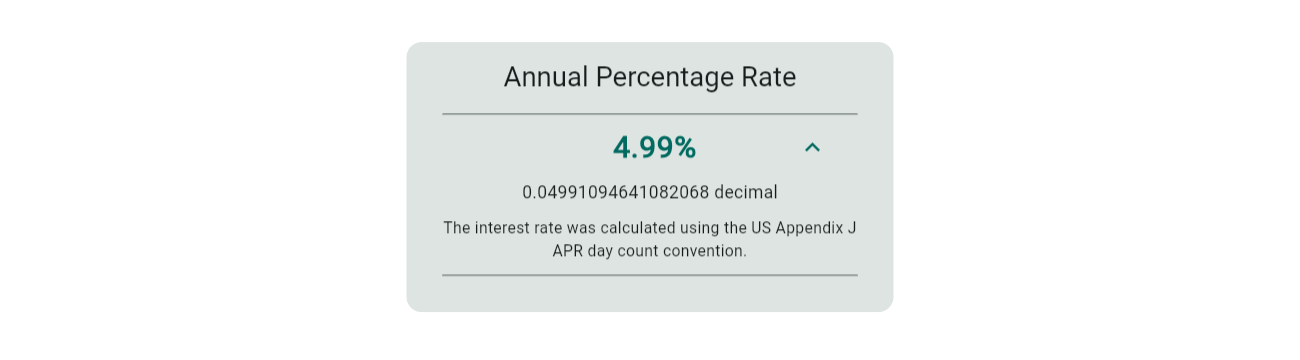
The interest rate to validate is found under the result summary tab:
To prove the interest rate (4.99% annual) is accurate, discount each value in the Amount column using the Discount Inputs ( $f$ ), ( $t$ ), ( $p$ ) and the annual interest rate ( $i$ ) (expressed as a decimal), then sum the results.
The discount formula and example calculations are provided below:
US Appendix J APR discount formula
$$ d = \frac{a}{(1 + f\frac{i}{p})(1 + \frac{i}{p})^t} $$ where:
- ( $d$ ) = Amount Discounted
- ( $a$ ) = Amount (to be discounted) from the schedule
- ( $i$ ) = Annual interest rate (decimal) from summary results
- ( $p$ ) = Number of unit-periods in a year (e.g., weeks, months) from the schedule
- ( $f$ ) = Additional days within a unit-period (fraction of a year for odd days) from the schedule
- ( $t$ ) = Number of complete unit-periods (e.g., weeks, months) from drawdown to cash flow, from the schedule
| Row | Formula Calculation | Amount Discounted ( $d$ ) | Balancing Total |
|---|---|---|---|
| 1 | $$\frac{-1000.00}{(1 + 0 \times \frac{0.04991094}{12})(1 + \frac{0.04991094}{12})^0}$$ | -1000.00 | -1000.00 |
| 2 | $$\frac{336.11}{(1 + 0 \times \frac{0.04991094}{12})(1 + \frac{0.04991094}{12})^1}$$ | 334.72 | -665.28 |
| 3 | $$\frac{336.11}{(1 + 0 \times \frac{0.04991094}{12})(1 + \frac{0.04991094}{12})^2}$$ | 333.33 | -331.95 |
| 4 | $$\frac{336.11}{(1 + 0 \times \frac{0.04991094}{12})(1 + \frac{0.04991094}{12})^3}$$ | 331.95 | -0.00 |
The Balancing Total column maintains a running total that should reduce to zero, though minor variations (±0.01) may occur due to rounding. Here, the total is -0.00, confirming the annual interest rate of 0.04991094 (4.99%) is correct for the US Appendix J APR convention.
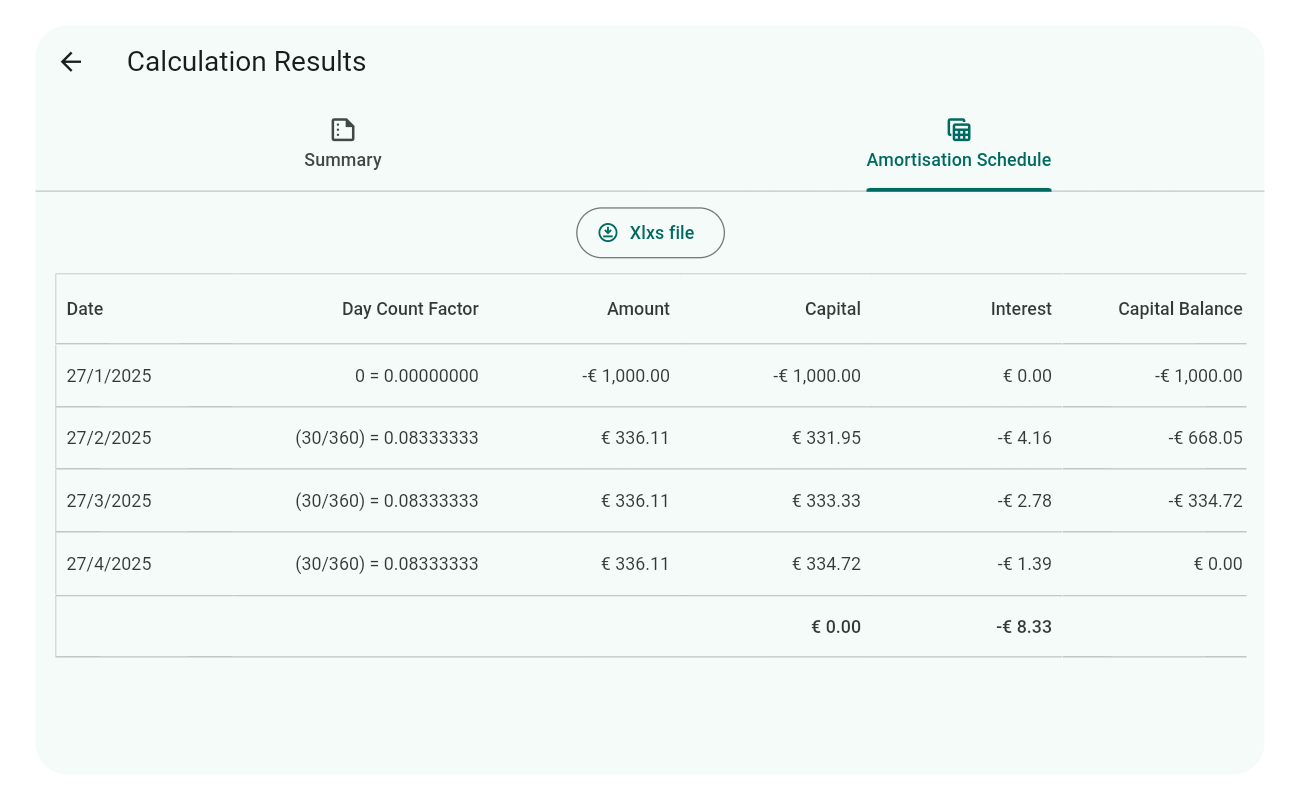
Amortisation Schedule
To validate the interest rate, we offer a simplified example of an amortisation schedule in the image below:
Notice the additional column after the Date column, which shows the Discount Inputs applied to each row. This column is hidden by default because day count factors can be confusing. To view it, tap or click 3 times on the Date column title. Repeat to hide it again.
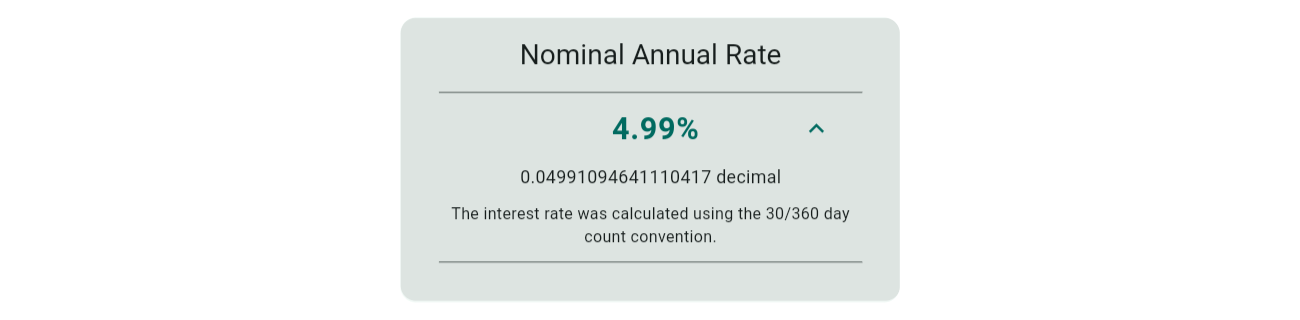
The interest rate you need to validate can be found under the result summary tab:
To confirm that the interest rate of 4.99% (as shown above) is accurate, you need to calculate the periodic interest for each row. Add this interest to the capital balance brought forward and the amount to determine the capital balance carried forward. Repeat this for each row until you reach the end.
Here’s the formula for periodic interest, followed by the step-by-step workings:
Periodic interest formula
$$ a = c \times i \times f $$ where:
- ( $a$ ) = Interest (periodic amount)
- ( $c$ ) = Capital Balance (brought forward)
- ( $i$ ) = Annual interest rate (decimal) from summary results
- ( $f$ ) = Day count factor from the schedule
| Row | Brought Forward ( $c$ ) | Interest Calculation $$( c \times i \times f )$$ | Amount | Capital Balance |
|---|---|---|---|---|
| 1 | 0.00 | $$0.00 \times 0.04991095 \times 0.00000000 = 0.00$$ | -1000.00 | -1000.00 |
| 2 | -1000.00 | $$-1000.00 \times 0.04991095 \times 0.08333333 = -4.16$$ | 336.11 | -668.05 |
| 3 | -668.05 | $$-668.05 \times 0.04991095 \times 0.08333333 = -2.78$$ | 336.11 | -334.72 |
| 4 | -334.72 | $$-334.72 \times 0.04991095 \times 0.08333333 = -1.39$$ | 336.11 | 0.00 |
In amortisation calculations, the final Capital Balance should ideally be zero, with minor deviations permitted due to rounding errors, thus proving the interest rate of 0.04991095 (4.99%) correct for the chosen 30/360 day count convention.
Tip
Even if you’re not interested in validating the interest rate, uncovering the Discount Inputs column can be helpful to see how the day counts are used in the calculation for your selected convention. Remember, the day count is based on the duration between the current and previous cash flow.